排序算法

Posted on | In |

冒泡排序

1
2
3
4
5
6
7
8
9
void Bubble_sort (int a[], int n) {
	for (int i = 0; i < n; i ++) {
		for (int j = i+1; j < n; j++) {
			if (a[i] > a[j]) {
				Swap(a[i], a[j]);
			}
		}
	}
}

Swap 函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void Swap(int  &a, int & b) {
	int tmp = 0;
	tmp = a;
	a = b;
	b = tmp;
}
//  or:
void Swap(int  &a, int & b) {
	if (a != b) {
		a ^= b;
		b ^= a;
		a ^= b;
	}
}

选择排序

1
2
3
4
5
6
7
8
9
10
void Select_sort(int a[], int n) {
	for (int i = 0 ; i < n ; i++) {
		min_index = i;
		for (int j = i+1; j < n; j++) {
			if (a[j] > a[min_index]) 
				min_index = j;
		}
		Swap (a[i], a[min_index]);
	}
}

直接插入排序

插入排序的思想有点像打扑克抓牌的时候，我们插入扑克牌的做法。想象一下，抓牌时，我们都是把抓到的牌按顺序放在手中。因此每抓一张新牌，我们都将其插入到已有的排好序的手牌当中，

当前抓到第i张牌key = a[i]，让其与排好顺序的i-1张牌，从后往前比较，大于key的话就往后移，直到遇到一个不大于key的牌，将key插入到这个位置后面。

1
2
3
4
5
6
7
8
9
10
11
void Insert_sort(int a[], int n) {
	for (int i = 1; i < n; i ++) {
		int key = a[i];
		int j = i -1;
		while (j >=0 && a[j]> key ) {
			a[j+1] = a[j];
			j--;
		}
		a[j+1] = key;
	}
}

希尔排序

先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。

其实希尔排序就是对相隔若干距离的数据进行直接插入排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void Shell_sort(int a[], int n, int step) {
	for (int gap = n/step;  gap > 0; gap /= step )
		for (int k = 0; k < gap; k++) {
			for (int i = gap; i < n; i += gap) {
				int key = a[i];
				int j = i - gap;
				While (j >= 0 && a[j]> key ) {
					a[j+gap] = a[j];
					j -= gap;
				}
				a[j+gap] = key;
			}		
		}
	}
}

归并排序

归并排序的主要思想是分治法（Divide and Conquer）。

首先考虑下如何将将二个有序数列合并。这个非常简单，只要从比较二个数列的第一个数，谁小就先取谁，取了后就在对应数列中删除这个数。然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可。

然后分治递归实现合并排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void mergearray(int a[], int first, int mid, int last , int temp) {
	int i = first, j = mid +1;
	int m = mid, n = last;
	int k = 0;
	while (i <= m && j <= n) {
		If (a[i] < a[j]) {
			temp[k++] = a[i++];
		} else {
			temp[k++] = a[j++];
		}
	}
	while (j <= n) 
		temp[k++] = a[j++];
	while (i <= m) 
		temp[k++] = a[i++];
		
	for (int i = 0; i<k; i++) {
		a[first+i] = temp[i];
	}
}
void Merge_sort(int a[], int first,  int last, int temp[]) {
	if (first < last) {
		int mid = (first + last) / 2;
		Merge_sort(a, first, mid, temp );
		Merge_sort(a, mid+1, last, temp );
		mergearray(a, first, mid, last, temp);
	}
}

快速排序

即挖坑填数+分治。

挖坑填数:

  1. i = l; j = r; 将基准数key挖出形成第一个坑 a[i]。
  2. j--由后向前找比它小的数，找到后挖出此数填前一个坑 a[i]中。
  3. i++由前向后找比它大的数，找到后也挖出此数填到前一个坑 a[j]中。
  4. 再重复执行2，3二步，直到i == j，将基准数key填入a[i]中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void Quick_sort(int a[], int l, int r) {
	if (l < r) {
		int i = l, j = r, key = a[l];
		while (i < j) {
			while(i < j && a[j] >= key) // 从右向左找第一个小于key的数
				j--;
          if(i < j)   
          	a[i++] = a[j];
          	
          while(i < j && a[i] < key) // 从左向右找第一个大于等于key的数  
          	i++;
          if(i < j)
          	a[j--] = a[i];
		}
		a[i] = key;
		Quick_sort(a, l, i - 1); // 递归调用
		Quick_sort(a, i + 1, r);
	}
}

堆排序

堆的定义

二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足两个特性：

  1. 父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。
  2. 每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆：

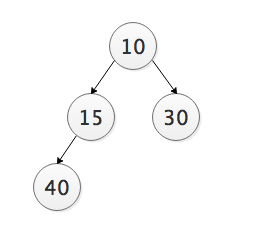
堆的储存

一般都用数组来表示堆，i结点的父结点下标就为(i–1)/2。它的左右子结点下标分别为2*i+1和2*i+2。如第0个结点左右子结点下标分别为1和2。上图堆的储存结构为：

10 15 30 40

堆的操作

  1. 建立堆：数组具有对应的树的表示形式。一般情况下，树并不能满足堆的条件，通过重新排列元素，可以建立堆化树。

    初始表： 40 10 30， 堆化树：10 40 30

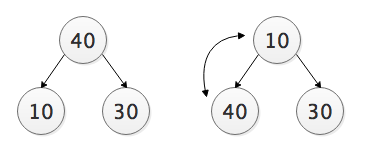
  2. 插入一个元素：新元素被加入到最底层，随后树被更新恢复堆，如下面将15加入表中。

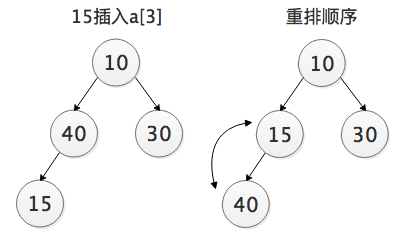
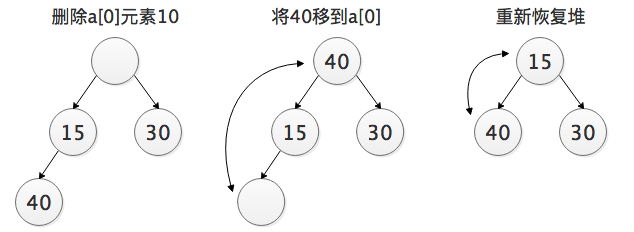
  3. 删除一个元素：删除总发生在根节点，最后一个元素用来填补空缺位置，结果树更新恢复堆。

由以上分析我们可以得知，插入操作其实就是一个从下往上调整的过程：
将元素插入到最后，从下往上与其父节点比较，小于父节点则交换，重复这个过程直到根节点。这是一个“上浮”的过程。

1
2
3
4
5
6
7
8
9
10
void Insert(int a[], int n, int num) {
	a[n] = num;
	FixUp(a, n);
}
void FixUp(int a[], int i) {
	while (int j = (i-1)/2; j>=0 && a[j] > a[i]; i = j, j = (i-1)/2) {
			Swap(a[i], a[j]);
	}
}

而删除操作则是一个从上往下调整的过程：
先删除根节点，将最后一个元素插入到根节点，从上往下与其左右节点比较，大于左右节点中最小的一个则交换，重复这个过程直到比左右节点都小，这时就不用调整了。这是一个“下沉”的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void Delete(int a[], int n) {
	Swap(a[0], a[n-1]);
	FixDown(a, 0, n-1);
}
void FixDown(int a[], int i, int n) {
	int j = 2*i+1;
	while(j < n) {
		if (j+1 < n && a[j+1] < a[j]) j++;
		if (a[j] < a[i]) Swap(a[i], a[j]);
		else break;
		i = j;
		j = 2*i+1;
	}
}

讲完FixUp和FixDown操作之后，给定一个无序数组，我们可以很方便的建立起一个堆。

从最后一个元素(n-1)的父节点开始，到根节点进行FixDown操作，就能建立起一个最小堆了。

1
2
3
4
5
void MakeMinHeap(int a[], int n) {
	for (int i = n/2-1; i >=0 ; i--) { 	//最后一个元素的父节点为((n-1)-1)/2, 即n/2-1
		FixDown(a, i, n);
	}
}

堆排序

首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据，重复上述步骤直至堆中只有一个数据时就直接取出这个数据。

由于堆也是用数组模拟的，故堆化数组后，第一次将a[0]与a[n-1]交换，再对a[0...n-2]重新恢复堆。第二次将a[0]与a[n–2]交换，再对a[0...n-3]重新恢复堆，重复这样的操作直到a[0]与a[1]交换。由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了。有点类似于直接选择排序。

1
2
3
4
5
6
7
void Heap_sort(int a[], int n) {
	MakeMinHeap(a, n);
	for (int i = n - 1; i >= 1; i--) {  
        Swap(a[i], a[0]);  
        FixDown(a, 0, i);  
    }  
}

注意使用最小堆排序后是递减数组，要得到递增数组，可以使用最大堆。

由于每次重新恢复堆的时间复杂度为O(logN)，共N-1次重新恢复堆操作，再加上前面建立堆时N/2次向下调整，每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N*logN)。故堆排序的时间复杂度为O(N*logN)。

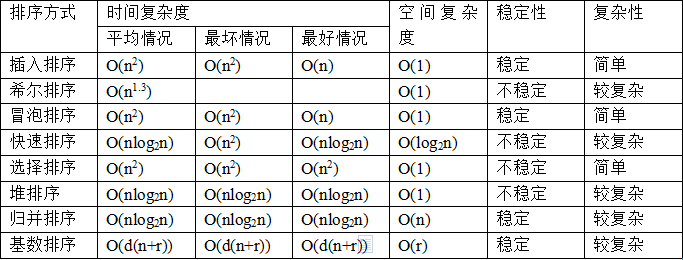
排序总结