本文主要是一篇系列视频观后总结,Essense of Linear Algebra 系列视频以几何的角度理解线性代数,形象地描述了线性代数的基本概念。视频原版位于Youtube,中英双语版可在BiliBili上访问。
一. 向量是什么 (What are Vectors?)
很精辟概括,一句话,
相加与数乘运算构成向量。
二. 线性组合 张成的空间和基 (Linear Combinations, Span and Basis Vectors)
线性相关(Linearly Dependent):
线性无关(Linearly Independent):
基的严格定义:向量空间的一组基(Basis)是张成(Span)改空间的一个线性无关(Linearly Independent)的向量集。
三. 矩阵和线性变换(Linear Transformation and Matrices)
变换和线性变换的定义
变换(Transformation)本质上就是函数(Function),接收一个向量(Vector Input),输出一个向量(Vector Output),变换是复杂的,可能将原本笔直的输入向量变得扭曲。
线性变换(Linear Transformation)则保持向量的加法和数乘运算。它有两条性质:
- Lines remain lines 直线依旧是直线
**注:不止平行与轴的直线,斜线(比如下图中的对角线)在变换后也应该是直线。
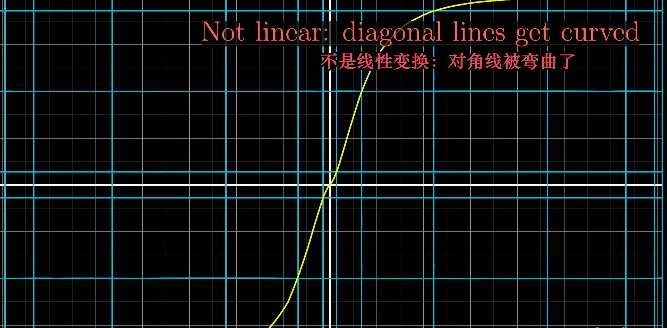
- Origin remain fixed 原点保持固定
在向量中,线性变换可以看作是保持网格线平行且等距分布。
这是在这里形象直观的定义,在本文的最后一节,我们将给出确切的抽象定义。当然,抽象定义并不只是适用于网格中的有方向的直线。
线性变换和矩阵的关系
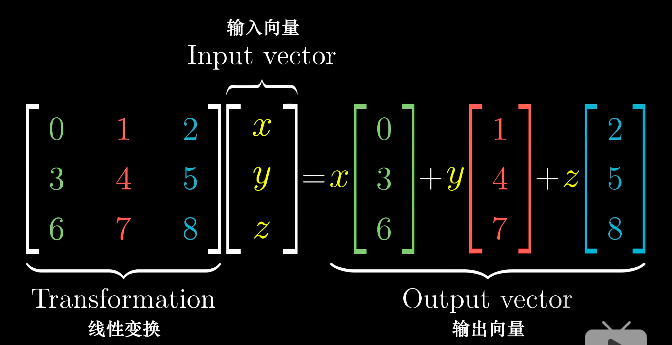
空间中的任意向量都可以用该空间的基向量线性组合表示。
一个二维线性变换可以由四个数字完全确定,即两个变换后的基向量i的坐标和基向量j的坐标,分别作为列向量组合成二维矩阵,就可以用矩阵表示一个线性变化,因此,
线性变换和矩阵是等价的。
一个矩阵与向量相乘就意味着对这个向量做了一次线性变换,
其中,[a, c] 为变换后基向量i的坐标, [b, d] 为变换后基向量j的坐标。
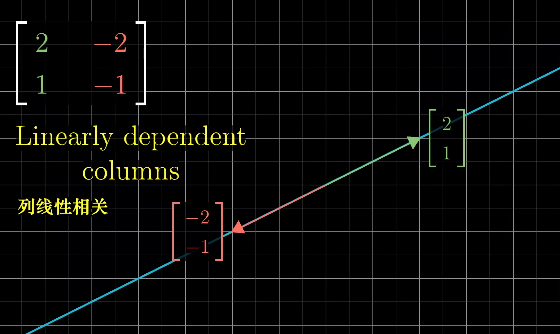
下图说明了一个具体的例子。

列线性相关
当变换后的两个向量线性相关时,空间会被压缩成一条直线。
三维空间下的线性变换
四. 矩阵乘法与复合线性变换(Matrix Multiplication as Composition)
由上一节的理解,我们其实可以很自然的推论出,两个矩阵相乘的几何意义,其实就是两个线性变换的相继作用。
过程是这样进行的,M1中的[e, g] 和[f, h]就是第一变换后的基向量,随后,M2作用于M1,即分别与第一次变换后的基变量相乘,由将这两个变量又进行了一次变换,最终得到二次变换后的基变量[ae+bg, ce+dg]和[af+bh, cf+dh]。
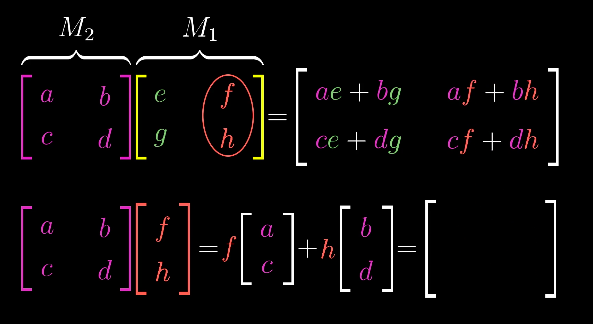
五. 行列式 (The Determinant)
行列式的几何意义
在二维空间中,当进行线性变换时,会改变基向量i和基向量j围成的单位正方形的形状,从而形成一个新的平行四边形。平行四边形面积的缩放比,就是代表线性变换矩阵的行列式大小。
行列式的方向,则取决于空间的定向,即满足右手定则为正,反之为负。对于二维矩阵,线性变换后的基向量i在基向量j的
右侧,则矩阵行列式为正,在左侧则为负。
三维空间中,行列式代表着1*1*1的单位立方体的体积缩放比例。
行列式的几何计算
二维空间中,由行列式和面积的关系,我们只要计算出变换后的平行四边形的面积,就可以求出行列式的大小,然后再根据空间定向确定其方向。
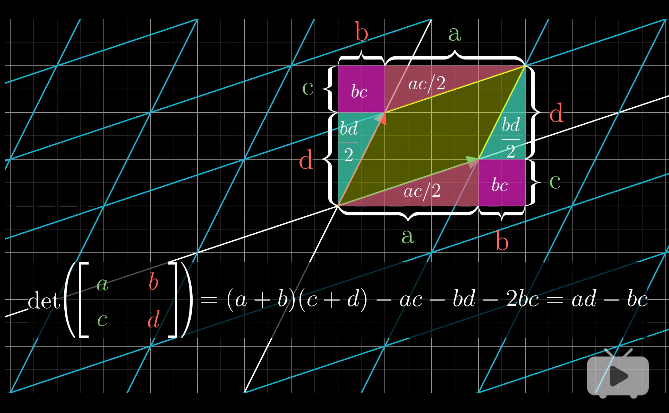
类似的,三维空间中,就是要计算出变换后平行六面体的体积,这里直接给出计算公式。(或许这个比直接套用行列式公式要复杂得多。。)

行列式为零
当行列式等于0,就意味着这个线性变换使得空间的维度降低了。
对于二维空间,有可能变换后的空间变成一维(一条直线),零维(一个原点)。
对于三维空间,有可能变换后的空间变成二维(一个平面),一维(一条直线),零维(一个原点)。
行列式为零的特性在后面的章节中有及其重要的作用。
六. 逆矩阵,秩,列空间和零空间 (Inverse Matrices, Rank, Column Space adn Null Space)
逆矩阵
首先,我们先引入线性方程组(Linear System of Equations)。

很显然能发现线性方程组和矩阵向量乘法相似。

这个方程的解依赖于矩阵A所代表的变换,是将空间压缩成一条线或者一个点的低维变换,还是变换成和初始状态一样的完整二维空间。由上节分析的结论,我们将它们分成两种情况,A的行列式为零,A的行列式不为零。
当
detA != 0时
要求出向量x,就需要将A的逆矩阵与向量v相乘,进行逆变换求出向量x的解。
也就是说,只要A的行列式为零,它的逆矩阵就一定存在。当
detA = 0时
空间被压缩成低维,这时不存在逆矩阵。但是却可能存在解,只要变换后的向量落在变换后的空间中。
秩和列空间
行列式这一节以及上述情况讨论,我们知道行列式为零代表着变换后的空间降维了,具体变成哪种低维度,但从行列式的值看不出来,因此,我们引入秩(Rank)的概念。
秩代表着变换后空间的维数。
三维空间中,一个变换矩阵的最大秩为3,这意味着基向量仍然能张成整个三维空间。
当变换后的空间被压缩成一个平面,则这个变换矩阵的秩为2;
当变换后的空间被压缩成一条直线,则这个变换矩阵的秩为1;
当变换后的空间被压缩成一个原点,则这个变换矩阵的秩为0。
不管是一条直线,一个平面还是三维空间,所有可能的变换的结果的集合被称为矩阵的列空间(Column Space)。
所有可能的输出向量的集合,叫做A的列空间。
我们已经知道,矩阵的列告诉我们基向量变换后的位置。列空间其实就是矩阵的列张成的空间。
所以更精确的秩的定义是:列空间的维数。
当秩最大时和列数相等,称之为满秩(Full Rank)。
零空间
零向量[0,0]一定在列空间中,当满秩时,唯一能在变换后落在原点的就是零向量本身。
但对于一个非满秩矩阵,它将空间压缩到一个更低的维度,
如果将一个二维线性变换将空间压缩到一条直线,那么沿着某个不同方向直线上所有的向量就会被压缩到原点。
如果将一个三维线性变换将空间压缩到一个平面,也会有某条直线上的所有向量被压缩到原点。
如果将一个三维线性变换将空间压缩到一条直线,则某个平面上的所有向量都会被压缩到原点。
变换后落到原点的向量的集合,被称为“零空间”(Null Space)或者 “核”(Kernel)。
对线性方程组来说,当时,零空间刚好是线性方程组的解。
七. 非方阵 (Nosquare Matrices as Transformation Between Dimensions)
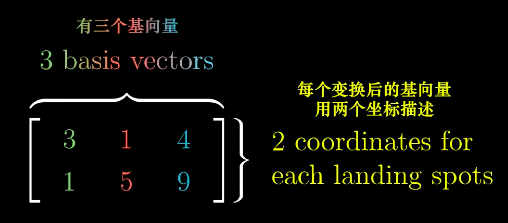
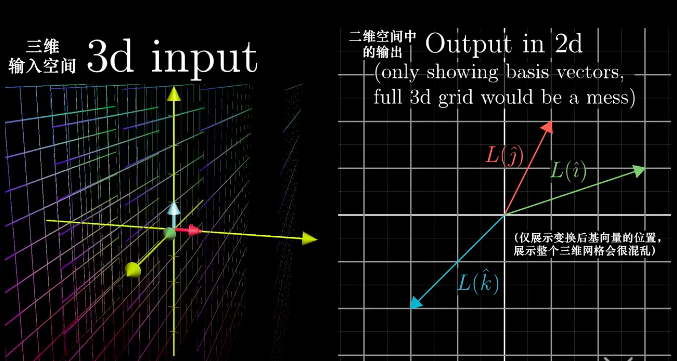
非方阵(Nosquare Matrices)可以进行不同维度空间中的转换。
二维升三维:

三维降二维:
八. 点积和对偶性 (Dot Product and Duality)
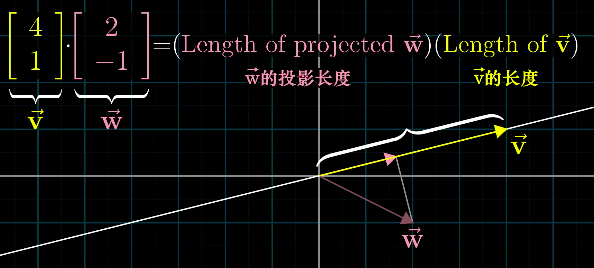
点积的几何意义是,
点积的大小:向量w在向量v方向的投影长度与向量v的长度的乘积。
点积的方向:根据两个向量的夹角确定,小于90度为正,大于90度为负。
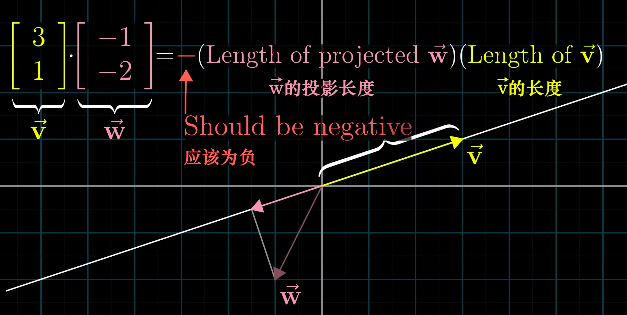
1X2变换矩阵的作用是将二维向量变成数轴上的一个数。1X2矩阵和二维向量之间存在着对偶性,点积可以转化成一个1X2矩阵作用在一个向量上。


九. 叉积 (Cross Product)
叉积的绝对值就是两个向量围成的平行四边形的面积。计算方法就是:矩阵的行列式。
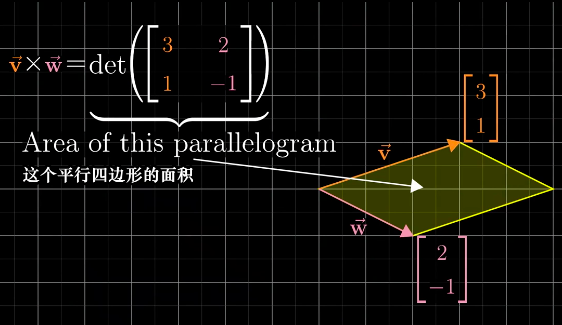
以上主要是针对二维空间中的向量而言,对于三维空间中的向量,叉积的计算与二维空间不同,它并不是输出一个有垂直于二维平面方向的数,而是接受两个向量,输出一个向量。它的公式是:


所以叉积严格的几何定义是,两个向量叉积产生的是第三个向量。向量的长度是两个输入向量张成的平行四边形的面积,向量的方向垂直于两个向量张成的平行四边形,正负取决于右手定则。
要理解这个公式的几何意义,是一个很有趣的过程。
假设两个三维空间中的向量v和w,我们采取以下步骤说明:
- 根据v和w定义一个三维到一维的线性变换。
- 找到它的对偶向量。
- 说明这个对偶向量就是
。
首先确定将叉积看成一个函数,对于任一输入变量[x, y, z],与一直的向量v和w组成任意平行六面体。

为什么把它看成一个函数呢?因为叉积运算具有一个非常重要的性质,它是线性的(线性的定义会在最后一节抽象出来)。一旦知道它是线性的,就可以用矩阵来描述这个函数。这个矩阵就是步骤1需要我们定义的三维到一维的变换矩阵。

看到这里,根据上一节的对偶性,有没有想将这个1X3矩阵与向量的乘法写成两个三维向量点积的冲动?

没错,到这里我们就完成了步骤2,将这个对偶向量定义为向量p。与此同时,我们也可以通过代数运算(待定系数法),解出向量p的值。

那么算出的这个向量p到底是什么呢?答案就是,这个向量p就是向量v与向量w的叉积!下面就是最有酷的一部分(Now for the Cool Part),步骤3了。
要理解p是什么,我们需要回顾之前的两个知识点。
- 行列式的几何意义
- 向量点积的几何意义
对于1,观察等式右边,是一个三维矩阵的行列式。它代表着由向量v,向量w和任意向量[x, y, z]组成的平行六面体的体积。
对于2,观察等式左边,向量p与任意向量[x, y, z]点积。它的几何意义是,将任意向量[x, y, z]投影到p上,然后将投影长度与p的长度相乘。
平行六面体的体积 = 向量v和w组成的平面面积 * 垂直于vw平面的高
p与[x, y, z]的点积 = p的长度 * [x, y, z]在p上的投影长度
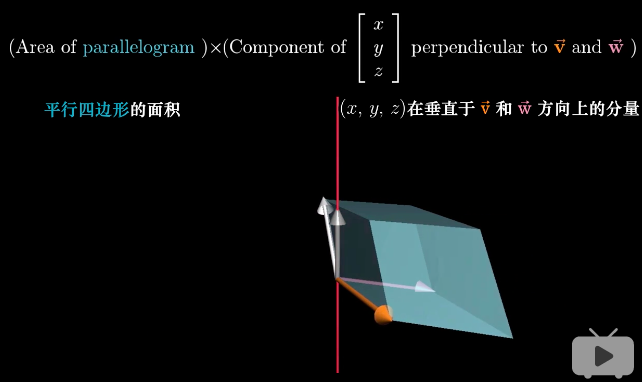
观察两个等式以及示意图,是不是发现了p到底是什么?很显然,p必然与vw垂直,并且长度等于两个向量张成的平行四边形的面积。往前翻一翻叉积的几何定义,神奇的发现与p的描述一致,
因此,这个向量p就是向量v和向量w的叉积。
十. 基变换 (Change of Basis)
基变换其实就是从自然坐标系([1, 0], [0, 1])变换到任一个坐标系([a, c], [b, d])的过程。这个变换矩阵就是
反过来的变换,则需要这个矩阵的逆矩阵。
例如在自然坐标系下的[-1, 2],在另一坐标系下就变成了[-4, 1]
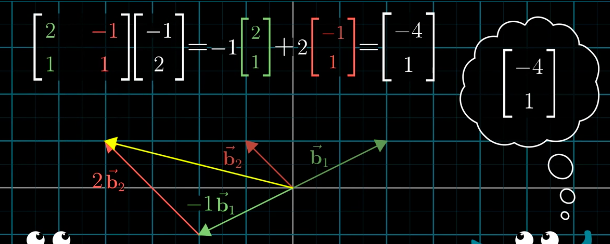
可以形象的描述成两种语言的翻译。
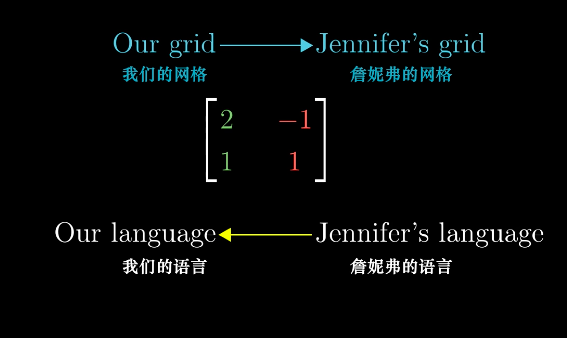

基变换的定义给了相似矩阵(Similar Matrix)直观的解释。

相似矩阵就是:用Jennifer的语言来表述变换后的向量。换句话说,实际上相似矩阵就是在不同坐标系下进行的相同的变换,因为变换相同,所以相似矩阵和原矩阵具有相等的行列式。
变换前后的向量都是在Jennifer的坐标系下,而中间的变换矩阵则是同一个变换,由图中颜色可知,这里代表着在自然坐标系下。
十一. 特征向量和特征值 (Eigenvectors and Eigenvalues)
特征向量几何意义
特征向量和特征值的几何意义:特征向量就是进行线性变换之后仍然留在它们所张成空间的向量,特征值就是这个向量拉伸的倍数,当向量反向时,特征值为负。

特征向量有什么应用呢?考虑一个三维空间中的旋转,如果你能找到这个旋转的特征向量,也就是旋转之后仍留在它所张成空间的向量,那么你就找到了它的旋转轴。
另外,像这个旋转的特征值必为1,因为旋转并不缩放任何一个向量。
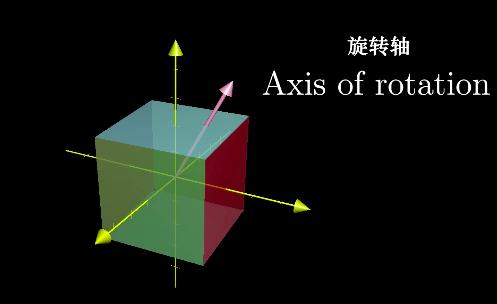
特征向量特征值的计算思想。
用符号表示的话,以下是特征向量的概念,

等式左边是一个矩阵向量乘积,右边则是一个向量数乘,经过一系列等式转化后,得出如果要求特征值,在特征向量非零的情况下,行列式必须等于0。从而求出特征值,最后,代入原表达式,利用线性方程组求出特征向量。

特征基
变换后的基向量正好是特征向量,则这组基被称为特征基(Eigenbasis)。
特征基变换矩阵是一个对角矩阵(Diagonal Matrix),所有的基向量都是特征向量,矩阵的对角元是它们所属的特征值。

对角矩阵有一个性质,n个相同对角矩阵相乘是比较好计算的,每个对角元都是自己的n次幂。

然而,如果要直接计算n个相同的非对角矩阵相乘,则是一件很痛苦的事。

所以很自然的想到,可不可以将一个非对角变换矩阵变成一个对角变换矩阵。答案是肯定的,只要这个非对角矩阵能选出一组特征向量来张成全空间的,那么就可以变换坐标系,使得这些特征向量就是基向量,而这个非对角变换矩阵将变成一个对角变换矩阵。
这个过程又叫做,相似对角化。
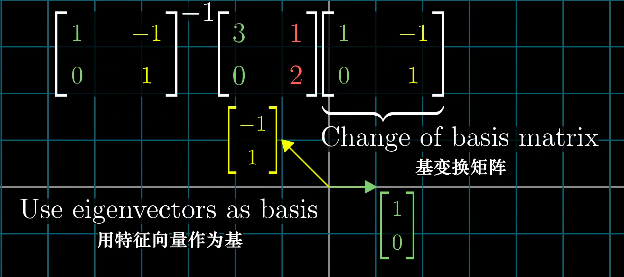

因此n个非对角矩阵相乘,就可以先计算相似对角化后的对角矩阵相乘,再通过基变换变回自然坐标系下的结果,计算复杂度就简便了很多。
当然,并不是所有的非对角矩阵都能相似对角化,矩阵的特征向量必须足够多,满足可以张成一个全空间。比如剪切矩阵就只有一个特征向量,数量不够,无法相似对角化。
十二. 抽象向量空间 (Abstact Vector Spaces)
最后的最后,我们回到最初的问题,什么是向量?(What are vectors?)。
相加与数乘运算构成向量。
我们上面讨论的向量都是一个箭头或者一组数字,从某种意义上来说,函数(Function)也是一种向量。函数拥有相加的性质,以及与实数数乘的性质。同时,函数的线性变换有一个完全合理的解释,那就是导数。
这里,我们终于可以给出线性的严格定义而不是以网格来描述了,这是一个由直观到抽象的过程。满足以下两条性质的变换是线性的,这两条性质是“可加性”和“成比例”。
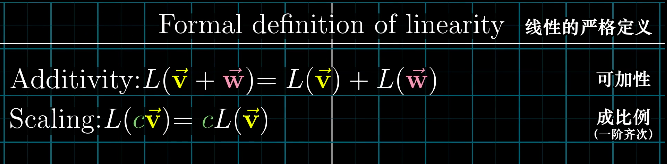
求导运算满足以上两条性质,所以它是一种线性变换。而只要是线性变换,都可以用矩阵表示,这是本文最重要的一个思想。因此,我们可以将求导运算抽象成矩阵与向量相乘的运算。
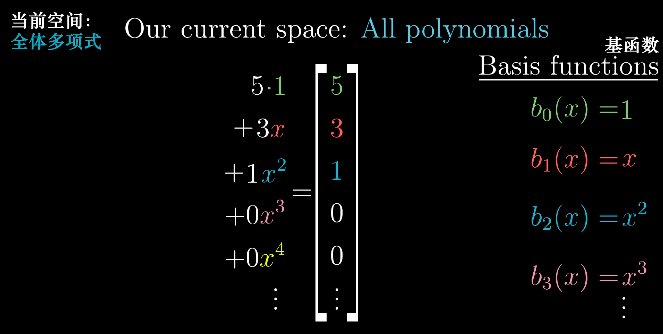

乍一看毫不相关的两者,其实是一家人。实际上我们讨论的线性代数中的一些概念,在函数中都有直接的类比。

回到“向量是什么”这个问题上来,数学上有很多类似向量的事物,只要你处理的对象集具有数乘和相加的概念,不管是空间中的箭头,一组数,还是函数的集合,甚至是你自己定义的某些奇怪的东西,线性代数所有关于向量,线性变换和其他的一些概念都应该适用于它。这些类似向量的事物构成的集合被称为“向量空间(Vector Space)”。
如果你作为数学家,可能很想说,
“大伙听好了,我可不想考虑你们构思出来的乱七八糟的向量空间!”
所以你需要做的事建立一系列向量加法和数乘必须遵守的规则,这些规则被称为“公理(axioms)”。

如果要让所有已建立好的理论和概念适用于一个向量空间,它必须满足这八大公理。
这,就是数学家眼里的“向量”。
它是抽象的,普适的。